Fast-Paxos is an optimization for the Paxos consensus protocol, Fast-Paxos eliminates one one-way delay by using larger quorum. Lamport explains Fast Paxos as an important building block for Generalized Paxos. Further, many advances consensus (or replication) protocols extend the idea of Fast Paxos to build leaderless consensus protocol, such as EPaxos. In this article, I will explain how Fast Paxos works.
Actors and Normal Message Flow
Before discussing the message flow in Fast-Paxos, let’s discuss the actors and the ballot number in Fast-Paxos.
As in Paxos, there are three main actors in Fast-Paxos: proposer, acceptor, and learner.
The proposer is responsible to propose valid values, the acceptor is responsible to
accept value under certain conditions, and the learner is responsible to handle the chosen value1. As in Paxos, to support $f$ failed machines, we need $f+1$ proposers, $2f+1$ acceptors, and $f+1$ learners. Typical deployment co-locates all kinds of actors in each machine, i.e. each machine simultaneously hosts proposer, acceptor, and learner. The figure below illustrate this typical deployment.
Typical Deployment for Paxos and Fast-Paxos
Additionally, in Fast-Paxos, other than the proposer, the client can directly propose values! this is the key reason why Fast-Paxos can eliminate one one-way delay. However, to ensure safety 2, the quorum requirement need to be adjusted to accommodate this direct proposal from the client; we’ll discuss this later.
Unlike Paxos, Fast-Paxos has two types of rounds: fast round and classic round. Respectively, each type of round is represented with fast round ballot number $b_f$ and classic ballot number $b_c$. Using integer ballot number, round 0 is automatically considered as a special fast round, i.e $b_f=0$.
Let’s see how Fast-Paxos achieve consensus in three one-way delays.
Initialization
The protocol starts even before the client propose values. The proposer initializes a fast round as illustrated in the figure below.
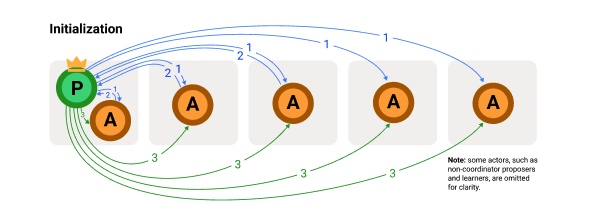Initialization in Fast-Paxos: Phase1A, Phase1B, and Phase2A. The coordinator is adorned with a crown.
- First, a proposer send prepare messages with ballot number for starting a fast round: $\texttt{Phase1A(}b_f\texttt{)}$.
- The acceptor responds the prepare messages (with $\texttt{Phase1B(}b_f\texttt{)}$) only if it has not received prepare messages from higher round. The acceptor promises not to participate in any lower round.
- The proposer waits for a majority of responses from the acceptors ($f+1$ acceptors). Then, the proposer propose a special value $\texttt{ANY}$ to all the acceptors, along with its fast round ballot number: $\texttt{Phase2A(}b_f\texttt{, ANY)}$. Here, we call the proposer that already received majority responses as the coordinator of a round.
At the end of this initialization, acceptors that already recieved the special value $\texttt{ANY}$ can accept any value proposed by a client, without the proposer involvement.
Note that we can skip the initialization altogether for round 0! That is, the acceptors are initialized to participate in round 0 and already accepted the special value $\texttt{ANY}$. This is possible since there is no lower round than round 0, thus no chosen value is possible in lower round. This is why round 0 is considered as a special fast round in Fast-Paxos.
Getting a Value Chosen
After the initialization, a client can directly propose value to the acceptors. The message flows is illustrated in the figure below.
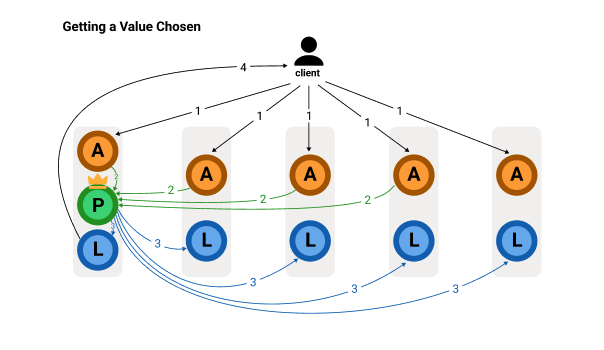Getting a value chosen in Fast-Paxos, the acceptor postpones sending Phase2B until it receives value from a client.
- When a client want to propose value $v$, the client sends $v$ to all the acceptors: $\texttt{ClientPropose(}v\texttt{)}$.
- When an acceptor receives a value $v$ from a client, the acceptor ignores $v$ if it has not accepted the special value $\texttt{ANY}$ or it already accepted another client’s value (already replaced $\texttt{ANY}$ with a different value). Otherwise, the acceptor votes for $v$ by replacing $\texttt{ANY}$ with $v$ and sending $\texttt{Phase2B(}b_f, v\texttt{)}$ to the coordinator of round $b_f$ (proposer that leads round $b_f$).
- When the coordinator of round $b_f$ receives $\texttt{Phase2B(}b_f, v’\texttt{)}$ from $3/2f+1$ acceptors for the same value $v’$, then the value $v’$ is chosen. The coordinator then notifies the learners and the client (in 4).
We can see this process to get a chosen value as a delayed Phase2B since in the initialization the coordinator already run Phase1A, Phase1B, and Phase2A. In Phase2A the coordinator proposes the special value $\texttt{ANY}$, the acceptor is delaying to respond with Phase2B until it receives the first value from a client.
Note that a client is notified that its proposed value $v$ is chosen in only three one-way delays: messages 1, 2, and 4; message 3 is local on the coordinator’s machine.
However, this run assumes $3/2f+1$ acceptors first receive the same value $v$ before receiving other values from other clients! In step 3 above, the coordinator can receive different conflicting values from the acceptors. If the coordinator receives conflicting values, it needs to do the recovery process, we call this as the slow path and I will explain this next.
Recovery: The Slow Path
When the coordinator finds out that $3/2f+1$ of the Phase2B messages contain different values, consensus is failed in the corrdinator’s current ballot number. In the recovery process, the coordinator needs to find a value that is safe to be proposed in the next higher round. Fast-Paxos has two kinds of recovery process: Uncoordinated and Coordinated.
Uncoordinated Recovery
The uncoordinated recovery is the simplest recovery process. The coordinator just need to fallback to the ordinary Paxos protocol by running Phase1 and Phase2 with higher ballot number. This recovery process also applies when the coordinator is crashed and another proposer trying to run the Paxos protocol.
However, how does the proposer choose the correct value to propose? This is an issue since in the same round (especially fast round) there could be multiple different values accepted by the acceptors! For example, in round 0, acceptor $a_1$ accepted value $v_a$ while acceptor $a_2$ accepted value $v_b$. This is possible when there are two different clients proposed different values $v_a$ and $v_b$.
Let’s handle this by listing all the possibilities. When a proposer completes Phase1 of Paxos (in a classic round), the proposer receives $f+1$ promises, some promises may contain different ballot number and different accepted values. A promise is in the form of Phase1B($b_c$, $vr$, $vv$), where $b_c$ is the proposer’s current ballot number, $vv$ is the value previously accepted in round $vr$. We call the remaining $f$ acceptors that do not respond (or late to respond) as the non-responding acceptors.
-
Case-1: From the $f+1$ acceptors, there is no value accepted yet. As in Paxos, the proposer is free to propose any value it wants in Phase2A.
-
Case-2: From the $f+1$ acceptors, there is the highest classic round’s ballot number $b_c$ with accepted value $v’$. As in Paxos, the proposer has to repropose the value $v’$ in Phase2A since $b_c$ is the highest ballot number among the $f+1$ promises.
-
Case-3: From the $f+1$ acceptors, there is the highest fast round’s ballot number $b_f$ and all the $f+1$ acceptors accepted the same value $v’$. In this case, the proposer has to propose $v’$ in Phase2A since it is possible that the non-responding $1/2f$ acceptors also accepted the same value $v’$. That is, it is possible that $3/2f+1$ acceptors accepted the same value $v’$ making $v’$ as the chosen value.
-
Case-4: From the $f+1$ acceptors, there is the highest fast round’s ballot number $b_f$ and the $f+1$ acceptors accepted different values.
- Case-4a: Among the $f+1$ acceptors, some $1/2f+1$ (or majority of $f+1$) acceptors accepted the same value $v’$ and one of them participated in round $b_f$. In this case, the proposer has to propose $v’$ since it is possible that the non-responding $f$ acceptors also accepted the same value $v’$. That is, there is already $3/2f+1$ acceptors accepted the same value $v’$ in the same round $b_f$, making $v’$ as the chosen value.
- Case-4b: Otherwise, no value is chosen yet so the proposer is free to propose any value in its classical round.
To give a concrete example, let assume deployment with even ballot number for fast round and odd ballot number for classic round. That is, {0, 2, 4, 6, …} are the possible ballot numbers for fast round and {1, 3, 5, 7, …} are the possible ballot numbers for classic round. All the cases above are illustrated in the figure below.
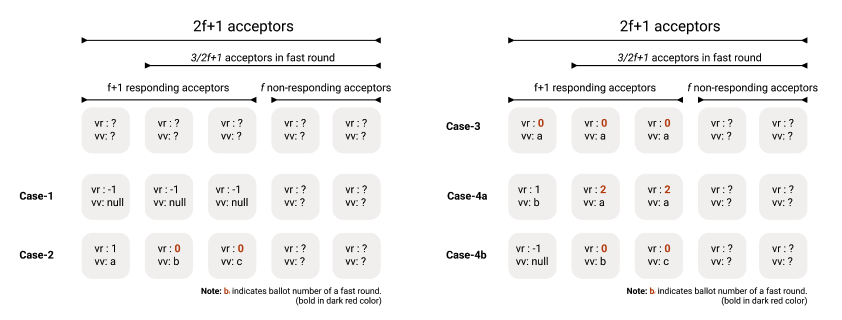Possible cases during recovery in Fast-Paxos.
Coordinated Recovery
The coordinated recovery in Fast-Paxos configures the proposers so the adjacent fast and classic round always handled by the same proposer. For example, the proposer in machine-1 is the owner of ballot number {0,1,10,11,20,21,…} and the proposer in machine-2 is the owner of ballot number {2,3,12,13,22,23,…}. Note that the coordinator of round 0 is also the proposer for round 1.
This configuration enables us to skip Phase1 in the uncoordinated recovery, and in turn eliminating two one-way delays! That is because the Phase2B messages of round 0 also act as Phase1B messages of the classic round 1. Since there is no ballot number between 0 and 1, it is safe for the coordinator to do this optimization. Specifically, similar with Phase1B message, Phase2B message also prevents the acceptor to participate in lower round (a promise) while also informing the previously accepted value.
When the coordinator receives $3/2f+1$ Phase2B messages (or alternatively, reach timeout after receiving $f+1$ Phase2B messages) and not all of them contain the same value, then the coordinator can directly handle the conflicting values as the rules in the uncoordinated recovery that I explain previously (Case 1-4).
In the end, the coordinated recovery only adds at least two one-way delay, compared to the addition of four one-way delays in the uncoordinated recovery.
Alternative Message Flows
The previous message flow is the message flow as what Lamport explained in his paper. There are multiple variants that we can have with Fast-Paxos.
First, the client does not have to broadcast the value to all the acceptors, the client can contact a single machine (the coordinator) that will do the broadcast for the client. This is the typical client-server deployment where the client only needs to talk to a single server (replica).
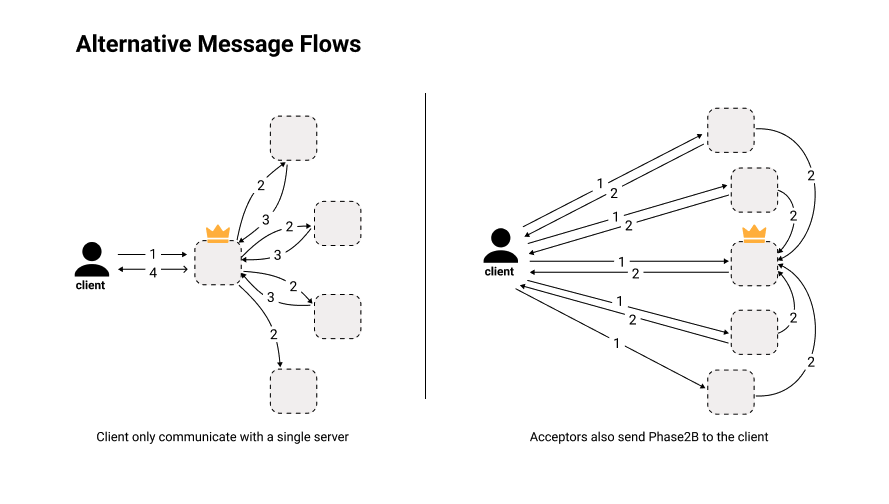Alternative message flows in Fast-Paxos.
Alternatively, the acceptors can also send the Phase2B messages to the client, while sending them to the coordinator. The client can deduce the chosen value after receiving $3/2f+1$ responses from the acceptors in two one-way delays only! This is useful if the client propose a blind value, a value that require no immediate execution. Example of a blind value is a put command that does not return any value, however the client still needs to know whether the put command is chosen or not.
Closing
In this article, I explain about Fast-Paxos that enables consensus under three one-way delays (or two one-way delays for blind value). However, using the protocol for replicated state machine (RSM) is not straightforward. In RSM, the replicas need to agree on the sequence of commands in a log; we run consensus for each slot in the log. Since the client directly propose values to all the acceptors, the value can end up in different slot in the log! This results in a lot of conflicting values.
Previous work, Speculative Paxos3, extends the idea of Fast-Paxos for RSM using speculative execution. Clients directly send commands to the replicas which speculatively execute the commands, then the replicas directly send the speculative execution results back to the client (Similar with the last alternative message flow that I explained previously).
Advanced replication protocol, such as EPaxos, uses dependency graph, instead of a log, to reduce the conflicting values. The dependency graph also makes such protocol more complex than its counterpart (MultiPaxos, Raft). Take a look at this tutorial paper that explains how EPaxos works.
In the next article, I will cover the quorum requirement in Fast-Paxos, and why we need $3/2f+1$ acceptors as the quorum in the fast round. Stay tuned!
Footnotes:
-
In replicated state machine (RSM), the learner is reponsible to execute the chosen value which commonly is RSM command (e.g
SET X 10,ADD X 13, etc). ↩ -
Safety: at most one value is chosen. Another way of saying safety: when a value $v$ is chosen in round $i$, then any round $j>i$ always propose the same value $v$. ↩